https://www.youtube.com/playlist?list=PLX2gX-ftPVXWgcF0WATMDr-AfvfaYjJZ3
why use Markov Chains?
- perdict the future by the distribution of probabilities.
- this is already used in Decsion systems. (Marketing, etc)
\[ X_{t+1} = P X_t \]
where \(P\) is the transition probability matrix (probability matrix), \(X\) is the distributions of states. 1 each item in the column (or row) will be the states.
we chain this, hence the Markov Chains.
- we iterate this to see the future states. \(t = 1,2,3 \cdot\)
- if we do this enough, some states converge, meaning that it is stabe distribution matrix.
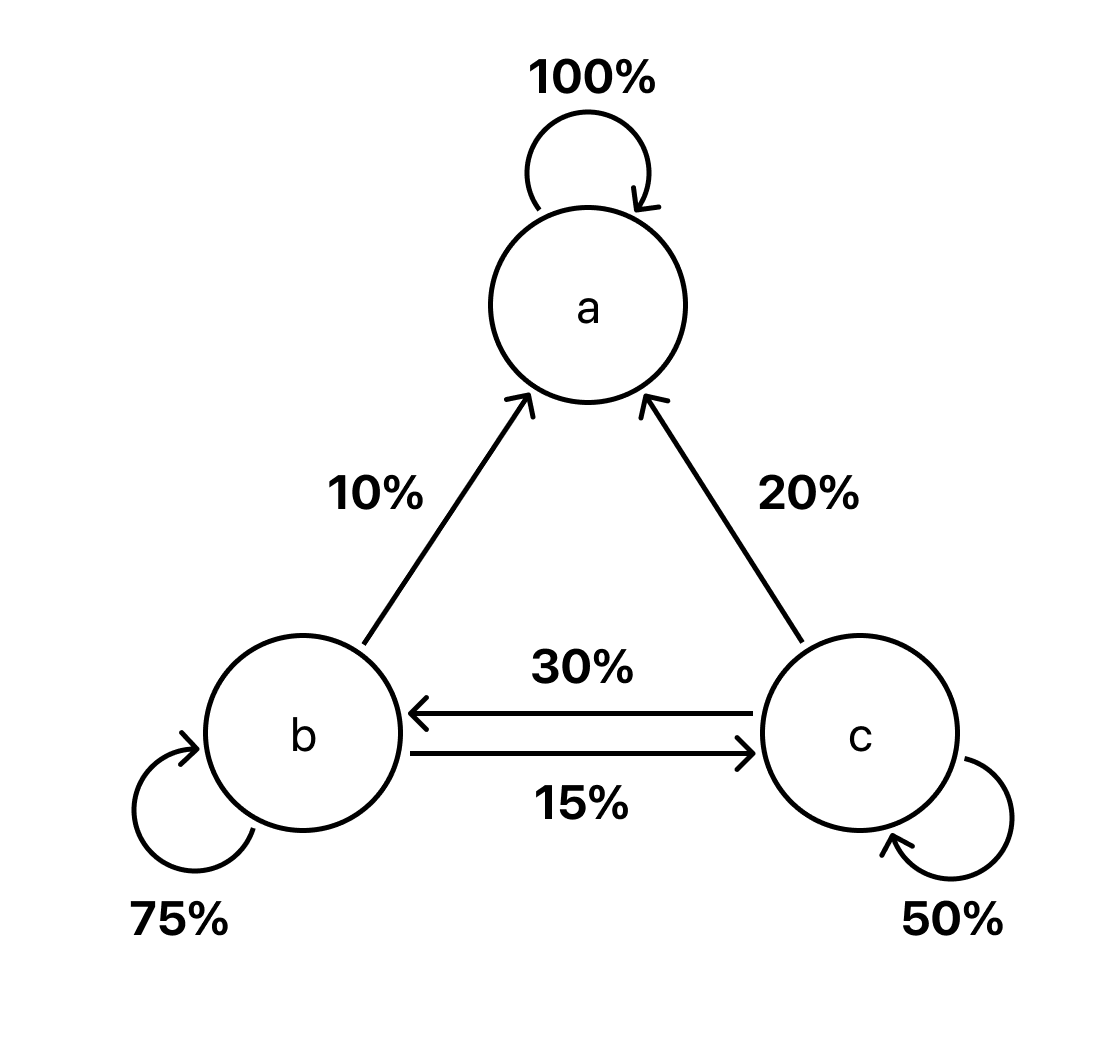
Properties of the Probability Transition Matrix
Stochastic…the sum of the vertical diection is 1.0. Regular…\(P^n\) (\(n>1\)), all elements are \(0<\).
… but there is a special type of Markov Chains that suck up all the population(or water) to several but a subset of states. This is an Absorbing Markov Chain. The transition matrix in this case will not conform regularity.
Absorbing Markov Chains
if \(P_{ij} = 1 (i=j)\), and all other probabilities in the column = 0, \(P_{i= 1 \rightarrow n, j} = 0 (i \neq j)\), then it is an Absorbing Matrix.
Canonical form of AMC
the Canonical form of the Absorbing Markov Chain can be illustrated like this, the ones are stacked in the right, so that it forms an identity matrix.
\begin{equation} V' = \left( \begin{array}{c|c} I & S \\ \hline 0 & R \end{array} \right). \end{equation}Footnotes:
some might show \(X_t P\) where \(P\) is transposed. For this material we use the \(PX_t\) since the probality matrix is easy to reason about.